No posts selected…
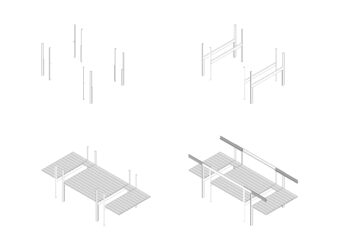
fig 668A 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 668B 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 668C 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 668D 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 668E 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 668F 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 668G 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 668H 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 668I 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 668J 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 668K 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667A 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667B 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667C 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667D 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667E 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667F 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667G 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667H 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667I 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667J 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667K 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667L 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
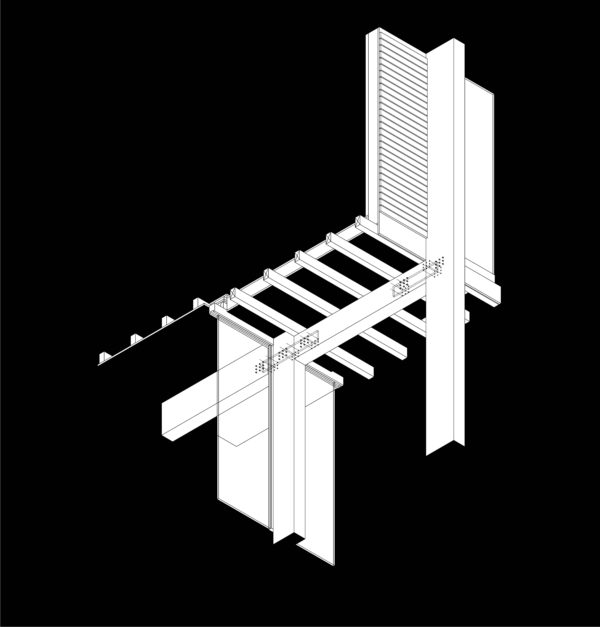
fig 609A Vynckier, posted by Wout Vandermeersch at 21.04.20 (filed under: steel)
fig 609B Vynckier, posted by Wout Vandermeersch at 21.04.20 (filed under: steel)
fig 609C Vynckier, posted by Wout Vandermeersch at 21.04.20 (filed under: steel)
fig 609D Vynckier, posted by Wout Vandermeersch at 21.04.20 (filed under: steel)
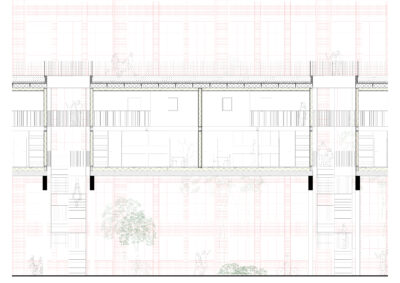
fig 597A Vynckier, posted by Wout Vandermeersch at 31.03.20 (filed under: brick)
fig 597B Vynckier, posted by Wout Vandermeersch at 31.03.20 (filed under: brick)
fig 597C Vynckier, posted by Wout Vandermeersch at 31.03.20 (filed under: brick)
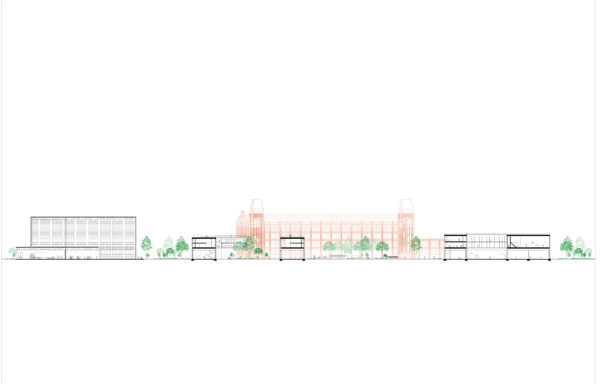
fig 596A Vynckier, posted by Wout Vandermeersch at 31.03.20 (filed under: brick)
fig 596B Vynckier, posted by Wout Vandermeersch at 31.03.20 (filed under: brick)
fig 596C Vynckier, posted by Wout Vandermeersch at 31.03.20 (filed under: brick)
fig 545A Vynckier, posted by Wout Vandermeersch at 05.03.20 (filed under: steel)
fig 545B Vynckier, posted by Wout Vandermeersch at 05.03.20 (filed under: steel)
fig 531A Bambow bridge – Atelier Lai, posted by Wout Vandermeersch at 26.02.20 (filed under: wood)
fig 530A Bambow bridge – Atelier Lai, posted by Wout Vandermeersch at 26.02.20 (filed under: wood)
fig 530B Bambow bridge – Atelier Lai, posted by Wout Vandermeersch at 26.02.20 (filed under: wood)
fig 668B 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 668C 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 668D 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 668E 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 668F 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 668G 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 668H 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 668I 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 668J 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 668K 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667A 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667B 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667C 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667D 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667E 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667F 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667G 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667H 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667I 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667J 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667K 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 667L 27/05, posted by Wout Vandermeersch at 26.05.20 (filed under: concrete)
fig 609A Vynckier, posted by Wout Vandermeersch at 21.04.20 (filed under: steel)
fig 609B Vynckier, posted by Wout Vandermeersch at 21.04.20 (filed under: steel)
fig 609C Vynckier, posted by Wout Vandermeersch at 21.04.20 (filed under: steel)
fig 609D Vynckier, posted by Wout Vandermeersch at 21.04.20 (filed under: steel)
fig 597A Vynckier, posted by Wout Vandermeersch at 31.03.20 (filed under: brick)
fig 597B Vynckier, posted by Wout Vandermeersch at 31.03.20 (filed under: brick)
fig 597C Vynckier, posted by Wout Vandermeersch at 31.03.20 (filed under: brick)
fig 596A Vynckier, posted by Wout Vandermeersch at 31.03.20 (filed under: brick)
fig 596B Vynckier, posted by Wout Vandermeersch at 31.03.20 (filed under: brick)
fig 596C Vynckier, posted by Wout Vandermeersch at 31.03.20 (filed under: brick)
fig 545A Vynckier, posted by Wout Vandermeersch at 05.03.20 (filed under: steel)
fig 545B Vynckier, posted by Wout Vandermeersch at 05.03.20 (filed under: steel)
fig 531A Bambow bridge – Atelier Lai, posted by Wout Vandermeersch at 26.02.20 (filed under: wood)
fig 530A Bambow bridge – Atelier Lai, posted by Wout Vandermeersch at 26.02.20 (filed under: wood)
fig 530B Bambow bridge – Atelier Lai, posted by Wout Vandermeersch at 26.02.20 (filed under: wood)